臺北市立西松高中 蘇惠玉教師
目前的高中數學教材中,已經不再教授開平方的直式開方法,在課綱中只要求學生會估計平方根的近似值即可。然而在統計部分的單元學習中,仍有些題目要求學生計算某些牽涉到平方根統計量的近似值,例如標準差。在筆者的教學經驗中,常有學生會問如何開平方根,因此筆者將在此篇文章中,以中國古算的開方術為基礎,介紹所謂的直式開方法。
《九章算術》〈少廣〉卷中有問:
今有積五萬五千二百二十五步。問為方幾何?
開方術曰:置積為實。借一筭,步之,超一等。議所得,以一乘所借一筭為法,而以除。除已,倍法為定法。其復除。折法而下。復置借筭,步之如初,以復議一乘之,所得副以加定法,以除。以所得副從定法。復除,折下如前。
這一段開方術,看起來不太好理解,由於古時候中算以算籌代筆,計算的過程實際上就是算籌的操弄,因此術文中有一些是算籌所帶來的難度,在此忽略不管。同時在劉徽的注釋中,他也提供了一個相當清楚簡潔的幾何解釋。
我們先以簡單的 144144 為例,如題目所言,假設一個面積為 144144 的正方形,如下圖。
由於十進位制的關係,100100 開方為 1010,因此先考慮十位數 aa。
由於 1010 的平方為 100100 最接近而不超過,因此開方後得十位數為 11。
從面積為 144144 的正方形中,扣除一個面積為 102=100102=100 的小正方形後,
剩下二個矩形與一個小正方形。
此時設下一位的個位數為 bb,小正方形的邊長則為 bb,
因此剩餘的面積 144−100=44144−100=44 應該要等於兩個矩形與小正方形的面積和,
故將先前得到的十位數 11 乘以 22 倍得 2020,
再考慮 bb,要使得 b(20+b)=44b(20+b)=44,因此得 bb 為 22,
因為 2×(20+2)=442×(20+2)=44,故得 144144 的平方為 1212。
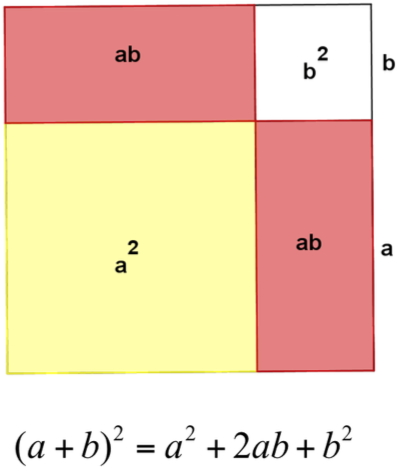

從幾何解釋中我們可以發現,當我們所求的平方根為二位數時,所用到的代數關係式即是
(a+b)2=a2+2ab+b2=a2+b(2a+b)(a+b)2=a2+2ab+b2=a2+b(2a+b)。
先猜測十位數字(1),減去其平方(100)之後,將此數2倍(1+1=2),再猜測個位數字。
而在上述所提少廣卷中的問題,求面積為55225的正方形邊長,估計所求的平分根為三位數,由
(a+b+c)2=a2+b2+c2+2ab+2ac+2bc=a2+b(2a+b)+c(2a+b+c)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc=a2+b(2a+b)+c(2a+b+c)
可知,此時開方所使用的方法與前面相同,只是多求1個位數而已。計算步驟如下:
- 將 5522555225 從個位數開始二位一撇作記號(定位),由此知所求平方根為三位數 a+b+ca+b+c
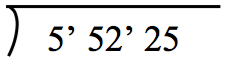
- 猜測最接近 55 的平方數為 2(a=200)2(a=200),從 5522555225 中減去 2002=400002002=40000,剩下 1522515225
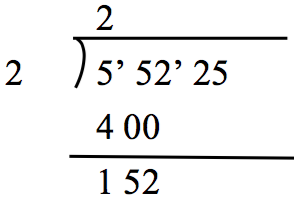
- 將 200200 自己加一次(22倍),考慮下一位數 bb,要接近而不超過 1522515225,得 b=30b=30,
從 1522515225 中減去 30×430=1290030×430=12900,剩下 23252325
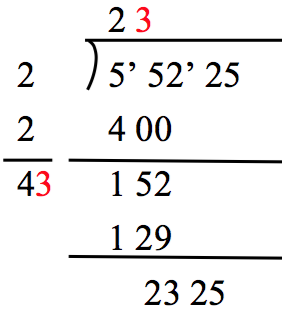
- 將 3030 再加一次(22倍),併入之前的結果得 460460,考慮下一位數 cc,
要接近 23252325 而不超過,得 c=5c=5,從 23252325 中減去 5×465=23255×465=2325,餘數為 00
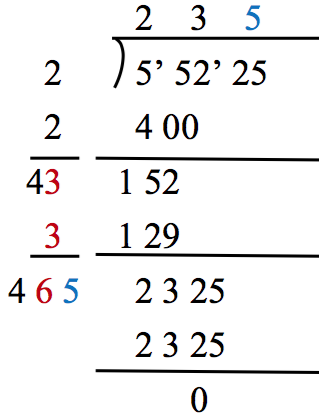
如果在個位數減完之後還有剩,則在個位數之後標示小數點,一次考慮兩個數字,繼續同樣的動作,直到得到想要的位數為止,例如求 52580−−−−−√52580,前面的步驟與上面相同,接下來如下:
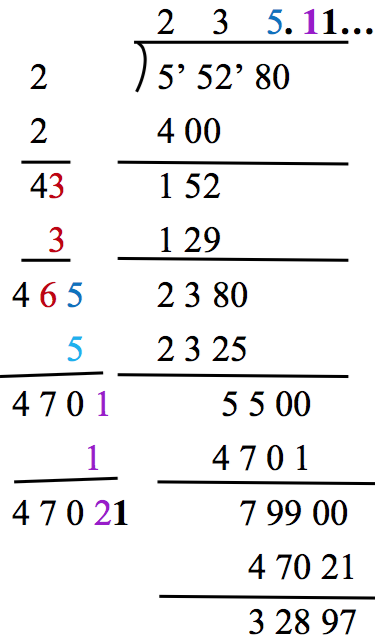
得到 52580−−−−−√≈235.1152580≈235.11。