http://www.phy.ntnu.edu.tw/demolab/phpBB/viewtopic.php?topic=8321&forum=60
所謂滾動,是移動+轉動的組合。當圓邊緣上某點(設為A點)繞圓心轉一圈(路徑=2πR) 時,圓心向前移動的水平位移亦是2πR,所以圓心水平移動速度與A點相對圓心的切線速度大小相同。
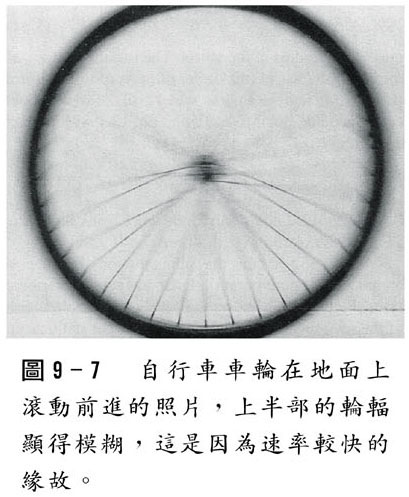
若我們站在地面觀察輪子的滾動,它是既轉動又移動的。而站在地面觀察輪子上任何點的運動,根據相對速度概念:v(點對心)+v(心對地)=v(點對地)---向量處理。
可知,為何上圖中,輪子上緣的攝影較模糊,而下緣是清晰的。
正上方點,對地速度v=(2πR/T)+(2πR/T)=2*(2πR/T)
正下方點:v=(2πR/T)-(2πR/T)=0
輪與地面接觸點,瞬時速度為零,此所以說:「滾動摩擦是靜摩擦」的原因。